Project Euler - Problem 14: Longest Collatz sequence

The following iterative sequence is defined for the set of positive integers:

n → n/2 (n is even)

n → 3n + 1 (n is odd)

Using the rule above and starting with 13, we generate the following sequence:

13 → 40 → 20 → 10 → 5 → 16 → 8 → 4 → 2 → 1

It can be seen that this sequence (starting at 13 and finishing at 1) contains 10 terms. Although it has not been proved yet (Collatz Problem), it is thought that all starting numbers finish at 1.

Which starting number, under one million, produces the longest chain?

NOTE: Once the chain starts the terms are allowed to go above one million.

Let build a simple function to generate a Collatz sequence given a starting number.

collatz_seq <- function(n) {
  out <- vector("integer")
  while (n != 1) {
    out <- c(out, n)
    n <- if (n %% 2 == 0) n/2 else 3*n + 1
  }
  c(out, 1)
}

collatz_seq(13)

##  [1] 13 40 20 10  5 16  8  4  2  1

lapply(1:10, collatz_seq) # first ten numbers

## [[1]]
## [1] 1
## 
## [[2]]
## [1] 2 1
## 
## [[3]]
## [1]  3 10  5 16  8  4  2  1
## 
## [[4]]
## [1] 4 2 1
## 
## [[5]]
## [1]  5 16  8  4  2  1
## 
## [[6]]
## [1]  6  3 10  5 16  8  4  2  1
## 
## [[7]]
##  [1]  7 22 11 34 17 52 26 13 40 20 10  5 16  8  4  2  1
## 
## [[8]]
## [1] 8 4 2 1
## 
## [[9]]
##  [1]  9 28 14  7 22 11 34 17 52 26 13 40 20 10  5 16  8  4  2  1
## 
## [[10]]
## [1] 10  5 16  8  4  2  1

One issue comes with the above implementation is that we have a growing objects1 out. This is inevitable because we don’t know when the Collatz sequence will converge, so the length of the final out is unknown. The cost is rising memory consumption which is eating up my humble computer’s RAM very quickly.

seq_size <- lapply(1:100000, function(x) {s <- collatz_seq(x); pryr::object_size(s)})
plot(1:100000, cumsum(seq_size)/1e6, type = "l")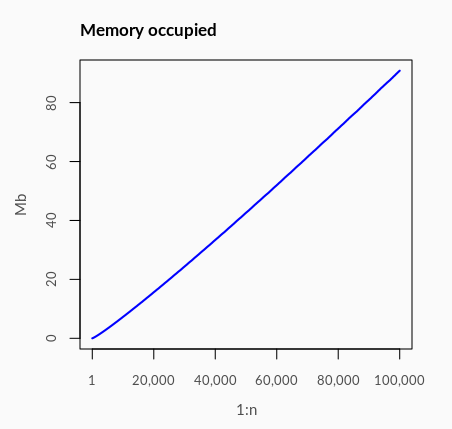

For this kind of computation, we can make use of parallel processing:

library(parallel)
n_cores <- detectCores()
cl <- makeCluster(n_cores)
col_seq <- parLapply(cl, 1:1e6, collatz_seq)
col_seq <- vapply(col_seq, length, integer(1))
which.max(col_seq)
## 837799